Mesurer la Terre - Chapitre 4

Quand la Terre rétrécit

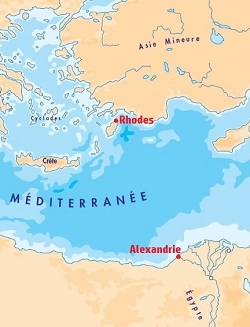
Laissons l'Egypte et ses habitants derrière nous et allons faire un peu de tourisme sur l'île de Rhodes, où le philosophe grec Posidonios d'Apamée (vers 135-51 av J.-C.) vient d'ouvrir une école de rhétorique (l'art de bien parler), école qui connaît d'ailleurs un certain succès puisque Pompée et Cicéron viennent parfois y suivre les leçons du maître. Rassurez-vous, nous y allons non pas pour écouter de beaux discours, mais parce que Posidonios s'est illustré dans un tout autre domaine : environ 150 ans après Eratosthène, ce dernier a lui aussi tenté de déterminer la longueur du méridien terrestre, en se basant sur l'observation de Canopus, étoile la plus brillante du ciel après Sirius. Observée depuis l'île de Rhodes, cette dernière ne fait que passer au ras de l'horizon, alors qu'elle atteint une hauteur maximale de 7,3° à Alexandrie.

La différence de latitude entre Rhodes et Alexandrie est donc d'environ 7°. Quant à la distance qui les sépare, Posidonios l'estime en tenant compte du temps de parcours d'une galère reliant ces deux destinations à vitesse normale : la méthode est donc proche de celle employée par Eratosthène, mais la précision est bien moindre. Ses résultats nous ont été transmis par Strabon : "D'après les mesures récentes de la Terre, celle ci est plus petite que prévu : Posidonius estime sa circonférence à environ 180.000 stades". Cela représente un peu moins de 30 000 kilomètres. Strabon ajoute ensuite qu'en naviguant vers l'ouest, on peut espérer atteindre l'Inde en parcourant moins de 70 000 stades, soit 11 000 km. Les valeurs obtenues par Posidonios, erronées car sous-estimant largement les distances réelles, seront reprises par d'autres savants et parviendront telles quelles à la Renaissance, ce qui ne sera peut-être pas sans conséquences...

Appréciation du bulletin : " Copie sur ses camarades ! "

Nous voilà transportés au IIe siècle après J.-C.. Retournons à la bibliothèque d'Alexandrie, où travaille alors l'un des plus grands savants de l'antiquité : Claude Ptolémée. Ce dernier est à la fois astronome, géographe, mathématicien, astrologue, et bien qu'il soit totalement nul en informatique, il mérite amplement notre respect.

Si l'histoire a retenu son nom, c'est avant tout pour son modèle géocentrique : la Terre, immobile, trône au centre de l'Univers, tandis que le Soleil, les planètes et les étoiles lui tournent autour en décrivant des cercles (plus précisément des combinaisons de cercles). Il n'est certes pas l'inventeur de ce modèle, en grande partie emprunté à l'astronome Hipparque, mais il l'a perfectionné. Ce travail nous a été transmis dans une oeuvre monumentale en treize volumes, la Syntaxe mathématique, plus connue sous le nom d'Almageste (la "Très Grande"), ouvrage qui fera autorité jusqu'à la fin du XVIe siècle.

C'est toutefois sa Géographie en huit volumes, rédigée vers l'an 150, qui va retenir ici notre attention. Vaste travail de compilation, elle fait état des connaissances géographiques du monde gréco-romain, sous le règne de l'empereur Hadrien
L'Empereur romain Hadrien (76 - 138), de la dynastie des Antonins, succède en 116 à Trajan, qui l'avait adopté sur son lit de mort. Homme parmi les plus lettrés de son temps, il voue une grande admiration à la culture grecque.
De tempéramment pacifiste, il renforce le limes, système de fortifications établies le long des frontières de l'Empire, qu'il espère ainsi protéger des Barbares. Le mur d'Hadrien, qui court sur 120 km entre l'Angleterre et l'Ecosse, est la portion la plus connue de ce dispositif de défense (visible ci-dessous).

. Dans le dernier volume, on trouve 27 cartes représentant l'écoumène, c'est à dire la totalité du monde habité connu à l'époque. Pour élaborer cet ouvrage, Ptolémée s'est là encore basé sur les travaux de ses prédécesseurs, en particulier ceux du géographe Marinos de Tyr. Ce dernier ayant lui-même repris les travaux de Posidonios d'Apamée, il n'est pas étonnant que Ptolémée ait à son tour sous-estimé la valeur de la circonférence terrestre, la ramenant lui aussi à environ 30 000 km.
Une autre source d'erreurs provient des récits de grands voyageurs, ces derniers ayant parfois tendance à en rajouter un peu, histoire d'embellir leurs exploits. Ceci a pour conséquence une surestimation de la taille de l'écoumène, Ptolémée considérant qu'il s'étend sur 180° de longitude, soit des îles "Fortunata" (sans doute les îles du Cap Vert) à la péninsule indochinoise. Cette surestimation de l'extension des terres va bien entendu conduire dans le même temps à sous-estimer la taille des océans.

Or, s'il faut en croire nombre d'historiens, Christophe Colomb se serait précisément appuyé sur les affirmations de Strabon et de Ptolémée (il possédait un exemplaire de sa Géographie) pour justifier la faisabilité de son expédition vers l'ouest. D'autres pensent toutefois qu'il aurait employé (sciemment ?) des unités de mesure incorrectes... Quoiqu'il en soit, l'idée reçue selon laquelle il dut convaincre ses pourvoyeurs de fonds de la sphéricité de la Terre est totalement fausse : elle remonte à l'écrivain Washington Irving (1783-1859), qui publia en 1828 un roman intitulé Histoire de la vie et des voyages de Christophe Colomb, dans lequel il invente de toute pièce la scène où Christophe Colomb doit faire face à des savants obscurantistes.

Si les universitaires de Salamanque doutent de la faisabilité de son voyage, c'est parce qu'ils connaissent, entre autres, les travaux d'Eratosthène, et qu'ils soupçonnent que la distance séparant l'Espagne de l'Inde en navigant vers l'ouest ne soit beaucoup trop grande pour être franchie avec les moyens dont on dispose à l'époque. Force est de reconnaître qu'ils avaient raison : si le continent américain n'avait pas été là, l'expédition de Christophe Colomb n'aurait pas eu l'ombre d'une chance d'atteindre l'Inde, totalement hors de portée de ses modestes caravelles.

Laissons le navigateur Génois à son expédition, et revenons à notre sujet. Tous les cartographes sont d'accord sur ce point : représenter une surface courbe sur un plan est une véritable gageure. Ptolémée fait toutefois preuve d'innovation dans ce domaine, introduisant dans un premier temps un système de projection conique en forme de manteau, avec une grille constituée de parallèles et de méridiens représentés par des segments de droites, système qu'il améliorera par la suite en représentant les méridiens par des arcs de cercles (carte ci-dessous). Ce sont au total près de 8000 lieux qu'il repère de la sorte dans sa Géographie, faisant appel à des termes tels que "latitude" et "longitude", toujours en usage de nos jours. Nous lui devons également l'orientation des cartes vers le Nord géographique (avant, elles étaient tournées vers l'Orient, d'où le terme "orienter"), ainsi que le tracé des parallèles correspondant à l'équateur et aux tropiques.

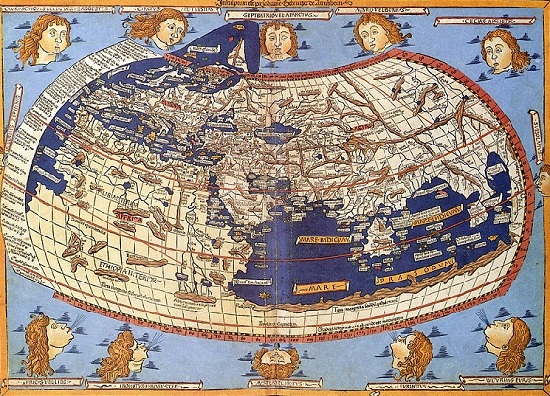
Le monde occidental va hélas perdre la trace de cette Géographie à partir du VIe siècle, même s'il semble que certains savants aient eu connaissance de son existence ainsi que d'une partie de son contenu lors de la période médiévale. Il faut attendre le tout début des années 1300 pour qu'un moine grec originaire de Constantinople, Maxime Planude, en redécouvre le texte, à partir duquel il va s'efforcer de redessiner les cartes. C'est ensuite à partir d'un manuscrit apporté à Florence depuis Constantinople que la Géographie sera traduite en latin, au début du XVe siècle. Elle sera alors progressivement redécouverte en Europe, l'invention de l'imprimerie contribuant à sa diffusion et à son succès.

Changement d'époque, changement de décors : nous allons maintenant faire un saut dans l'Inde du Xe siècle, où nous attend (en principe) l'érudit persan Abû al-Rayhan Muhammad Ibn Ahmad al-Biruni. Ce dernier vient en effet d'accomplir un véritable tour de force : il a paraît-il réussi à déterminer le rayon de la Terre à l'aide d'un simple astrolabe, d'une montagne, et d'une bonne dose de savoir faire...

Retour à l'introduction

Astronomie pour les myopes - Mentions légales