Mesurer la Terre - Chapitre 3

S'il semble acquis au IV^è siècle av J.-C. que nous vivons à la surface d'une immense sphère, nous ignorons par contre quelle est sa taille : immense, oui, mais à quel point ? C'est Eudoxe de Cnide (~ 406 - 355 av J.-C.) qui nous fournit l'une des toutes premières estimations, en déterminant la différence de latitude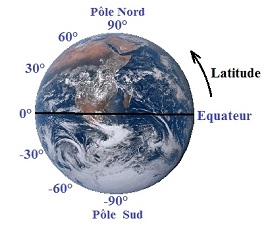

La latitude d'un point (sur Terre) est une coordonnée géographique qui correspond à la distance angulaire, exprimée en degrés, séparant ce point de l'équateur. Par définition, la latitude de l'équateur est nulle, soit 0°. Celle du pôle Nord est de +90°, tandis que celle du pôle Sud est de -90°, les latitudes étant considérées comme positives dans l'hémisphère Nord et négatives dans l'hémisphère Sud. entre deux lieux situés sur un même méridien (un méridien est une ligne imaginaire qui relie les deux pôles géographiques). Aristote va nous transmettre les résultats obtenus par Eudoxe dans son De Caelo (ou "Traité du Ciel") : le périmètre de la Terre vaut environ 74 000 de nos kilomètres actuels (l'unité de mesure alors en vigueur est le stade). Côté précision, cela reste très approximatif (la valeur exacte est de 40 008 km), mais il y a un début à tout.

Petite digression : alors que la Terre est généralement considérée comme étant fixe, Héraclide du Pont (388 - 315 av J.-C.) suggère que cette dernière tourne sur elle-même, expliquant ainsi le mouvement apparent des étoiles. Il ne s'arrête d'ailleurs pas en si bon chemin puisqu'il va jusqu'à proposer l'idée selon laquelle les planètes Mercure et Vénus tournent non pas autour de la Terre, mais autour du Soleil. Moins d'un siècle plus tard, Aristarque de Samos ira plus loin en affirmant que ce sont toutes les planètes, Terre comprise, qui décrivent des cercles autour du Soleil.

Et Eratosthène fut...

Poursuivons notre périple et rendons-nous dans la célèbre cité d'Alexandrie, ville phare (sans jeu de mot) de l'antiquité fondée en 331 av J.-C. par le conquérant Alexandre le Grand. A la mort de ce dernier, son général Ptolémée devient roi d'Egypte sous le nom de Ptolémée 1^er Soter et fonde une dynastie connue sous le nom de Lagides, qui règnera sur l'Egypte jusqu'à la mort de Césarion (Ptolémée XV, fils de César et Cléopâtre), assassiné en 30 av J.-C. par Octave, futur empereur de Rome. Mais nous nous égarons...

Vers 295 av J.-C. Ptolémée 1^er érige à Alexandrie une bibliothèque qui sera destinée à devenir la plus importante de l'antiquité. Agrandie par ses successeurs, on estime que sous le règne de Ptolémée III, elle contient près de 500 000 rouleaux de papyrus et parchemins. C'est ici qu'entre en scène Eratosthène (276 - 194 av J.-C.) : placé en 235 av J.-C. à la tête de la bibliothèque, celui-ci y exercera la fonction de conservateur jusqu'à sa mort. Ayant ainsi accès à l'ensemble des connaissances de l'époque, il se lance dans de nombreux travaux :

- il invente le terme "géographie", et étudie la répartiton des différentes zones climatiques,

- en mathématiques, il met au point une méthode permettant de trouver les nombres premiers, méthode connue sous le nom de crible d'Eratosthène,

- en astronomie, il établit un catalogue astronomique contenant plus de 600 étoiles et détermine la valeur de l'inclinaison de l'axe de rotation de la Terre.

Un tel CV suffirait déjà amplement à justifier sa notoriété, mais si l'Histoire a retenu son nom, c'est pour une toute autre raison. Il sait que le jour du solstice d'étéLe solstice d'été est le jour de l'année où le Soleil, dans son mouvement apparent sur la voûte céleste, atteint sa déclinaison maximale, autrement dit le jour où il passe le plus haut dans le ciel. Par conséquent, il s'agit du jour le plus long de l'année. Selon que l'année est bissextile ou non, le solstice d'été tombe le 21 ou le 22 juin. à midi (heure solaire), le Soleil passe exactement à la verticale de la ville de Syène (l'actuelle Assouan), puisqu'il peut alors éclairer directement le fond d'un puits. Or, au même instant, un gnomon (tige verticale qui projette son ombre sur une surface généralement plane) donne une petite ombre à Alexandrie, ce qui signifie que le Soleil ne passe pas à la verticale de cette ville. Eratosthène estime que l'ombre du gnomon forme par rapport à ce dernier un angle d'un cinquantième de cercle (soit 360° / 50 = 7,2°).
On raconte parfois qu'il aurait utilisé l'ombre du phare d'Alexandrie pour parvenir à ce résultat. Cette version de l'histoire a bien entendu le mérite d'être plus sexy que celle faisant intervenir un simple gnomon, mais au final on s'en flagelle le cristallin avec un trombonne à coulisse car cela revient strictement au même.
Nous pouvons constater sur l'image ci-dessous que cet angle (noté a1) correspond également à la différence de latitude (angle a2) entre les villes de Syène et d'Alexandrie, puisque ces deux angles ont la même valeur.

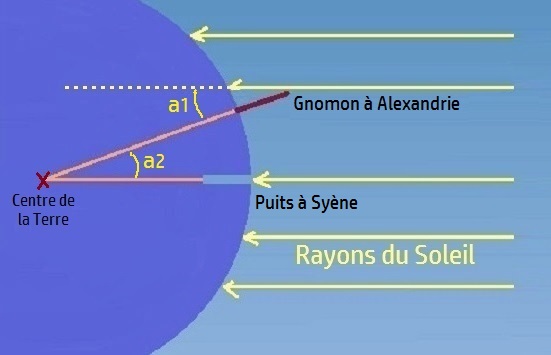
L'angle a2 (soit 7,2°) correspond donc à un cinquantième de cercle. Il ne reste par conséquent plus qu'à multiplier la distance Syène-Alexandrie par cinquante pour connaître la valeur de la circonférence terrestre. A priori, c'est un jeu d'enfants, mais nous allons voir que les choses sont loin d'être aussi simples...

Tout d'abord, le raisonnement d'Eratosthène n'est valable qu'à la condition que Syène et Alexandrie soient effectivement situées sur le même méridien, ce qui n'est pas tout à fait le cas. Le "petit" écart de longitude entre les deux villes conduit au final à une légère surestimation de la circonférence de la Terre (d'environ 2000 km). Ensuite, il faut connaître avec précision la distance qui sépare Syène d'Alexandrie, puisqu'elle sert de base au calcul d'Eratosthène. C'est là que les choses commencent à se compliquer. Primo, cela nécessite d'avoir un bématiste sous la main, c'est à dire un gars dont le boulot consiste à mesurer les distances entre villes.

Deuzio, il faut disposer d'un chameau, voire de plusieurs au cas où le premier tomberait en panne. En cette lointaine époque, comme il n'y a pas de satellites artificiels, c'est le chameau qui fait office de GPS, dont il est en quelque sorte l'ancêtre. En effet, il suffit au bématiste de compter les pas de ce noble quadrupède, à la marche très régulière, pour avoir une bonne estimation de la distance parcourue.

D'aucuns prétendent que cette histoire ne serait qu'une légende, mais une chose toutefois est certaine : le terme "GPS" découle directement de l'observation de la démarche du chameau, puisque ce dernier effectue de Grands Pas sur le Sable (bon, là on touche le fond, mais c'est ma tante Simone qui m'a obligée à écrire ça, moi je ne voulais pas).

Toujours est-il que la distance séparant Syène d'Alexandrie est estimée à 5000 stades. Cette ancienne unité correspondait, dit-on, à la longueur du stade d'Olympie, qu'Héraclès aurait déterminée en portant 600 fois ses pieds l'un devant l'autre. Seulement, nous ne connaissons pas la pointure d'Héraclès : chaussait-il du 39 ? du 45 ? du 59 ? Mystère... On pense toutefois qu'Eratosthène aurait employé le stade Egyptien, basé sur un pied de 0,2625 m, soit un stade de 157,5 m (0,2625 x 600). Dans ces conditions, 5000 stades correspondent à un peu moins de 800 de nos kilomètres. Quant à la circonférence de notre bonne vieille Terre, il est facile d'en déduire qu'elle doit valoir 250 000 stades (5000 stades x 50), soit 39 375 km, ce qui représente un écart d'environ 2 % par rapport à la valeur admise aujourd'hui ! En fait, Eratosthène aurait légèrement sous-estimé la distance séparant Syène d'Alexandrie, ce qui par chance compense sa première erreur (considérer que ces deux villes sont sur le même méridien).

Concernant ce résultat, deux remarques s'imposent : en premier lieu, il a été obtenu en attribuant au stade une longueur de 157,5 m, or rien ne prouve qu'Eratosthène ait utilisé cette valeur, différente d'une région à l'autre et pouvant varier de 149 m à 192 m. Dans ces conditions, la circonférence terrestre calculée par Eratosthène pourrait être comprise entre 37 000 km et 48 000 km. Qui plus est, le fait que la distance Syène-Alexandrie ait été estimée à 5000 stades, valeur toute "ronde", peut laisser planer quelques doutes quant à la crédibilté d'un tel résultat. Malgré cela, les travaux d'Eratosthène ne peuvent que susciter l'admiration, eu égard à la simplicité des moyens mis en oeuvre. Belle prouesse de la part d'un homme qui n'avait même pas le bac... Je dis chameau ! (pardon, chapeau !).

Encore un dernier point : les plus perspicaces sont en droit d'objecter que la validité de la méthode mise en oeuvre par Eratosthène repose sur l'hypothèse selon laquelle le Soleil est très éloigné de la Terre, assez éloigné en tout cas pour que les rayons qui nous en parviennent puissent être considérés comme parallèles entre eux. Or aux alentours de 430 av J.-C. (soit deux siècles plus tôt), Anaxagore de Clazomène
Philosophe grec né vers 500 av J.-C. à Clazomène, en Ionie, Anaxagore ouvre à Athène une école de philosophie, où il compte Périclès parmi ses élèves. Il introduit le concept de νοῦς (noûs), l'"Esprit", principe organisateur du monde, source de vie, de connaissance, de mouvement.
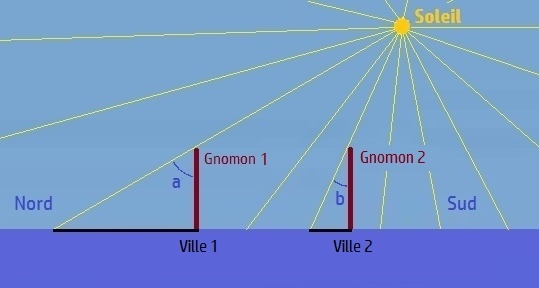
Considérant que les astres ne sont que des masses incandescentes et non des divinités comme l'enseigne alors la théologie, Anaxagore est condamné à l'exil (il évite la mort de justesse) vers 431 av J.-C.. convaincu de la platitude de la Terre, prétend au contraire que si la longueur de l'ombre d'un gnomon change avec la latitude du lieu d'observation, cela est justement dû à la relative proximité du Soleil (sur l'image ci-dessous, nous constatons en effet que l'ombre du gnomon est plus longue dans la ville 1, située plus au nord). Après avoir effectué quelques calculs, Anaxagore conclut que le Soleil est distant d'environ 6500 km, et que son diamètre ne dépasse pas 60 km. Beaucoup plus grave, il ose prétendre qu'il s'agit non pas d'une divinité, mais d'une simple boule de fer incandescent, ce qui lui vaut d'être condamné à l'exil à Lampsaque (son ami Périclès lui évite la peine de mort).

Dans ces conditions, pourquoi Eratosthène privilégia-t-il l'hypothèse d'une Terre sphérique située à grande distance du Soleil, plutôt que celle d'une Terre plate éclairée par un Soleil proche et de petite dimension ? Tout simplement parce que quelques années plus tôt, l'astronome et mathématicien Aristarque de Samos (~ 310 - 230 av J.-C.), réussit à estimer la distance Terre-Lune en se basant sur l'observation des éclipses lunaires, et arrive à la conclusion que cette distance vaut environ 20 rayons terrestres (il part du principe que la Terre est une sphère). Nous savons aujourd'hui que cette distance vaut en réalité 60 rayons terrestres, mais même en prenant le résultat obtenu par Aristarque, cela implique que le Soleil est au minimum à cette distance, puisque lors des éclipses solaires son disque est masqué par celui de la Lune (qui s'interpose entre la Terre et le Soleil). Aristarque va également tenter de déterminer la distance Terre-Soleil en faisant usage de méthodes géométriques, mais bien qu'il la sous-estime largement, il arrive à la conclusion que le Soleil est environ 19 fois plus éloigné que la Lune, et qu'il doit être près de six fois plus grand que la Terre. Ceci l'amènera à élaborer ce que l'on considère généralement comme le premier modèle héliocentrique de l'histoire occidentale : il place le Soleil au centre de l'Univers, et fait tourner tout le reste autour. Cette conception de l'Univers tombera malheureusement dans l'oubli pendant presque deux millénaires.

En conclusion, bien que l'on ne connaisse toujours pas (à l'époque) la distance qui nous sépare du Soleil, il semble raisonnable de penser qu'il est extrêmement distant de la Terre. L'hypothèse de départ d'Eratosthène, qui connait les travaux d'Aristarque pour avoir suivit ses cours d'astronomie et de mathématiques, est donc amplement justifiée. La fin de cette histoire est malheureusement tragique puisqu'Eratosthène, perdant petit à petit l'usage de la vue et ne le supportant pas, décide de mettre fin à ses jours : il cesse de s'alimenter et meurt d'inanition à Alexandrie, en l'an 194 av J.-C..

Retour à l'introduction

Astronomie pour les myopes - Mentions légales