Mesurer la Terre - Chapitre 5

Al-Biruni prend de la hauteur

C'est à proximité de la ville de Kath, dans une région appelée Khwarezm (au sud de la mer d'Aral), que nait Al-Biruni !, en l'an 973. Moins célèbre que certains de ses contemporains (Avicenne, Alhazen...), ce dernier va pourtant s'illustrer dans une foule de domaines : mathématiques, astronomie, botanique, histoire, géographie, philosophie, médecine, poésie, micro-informatique, et j'en passe... Il faut dire qu'il reçoit une éducation solide : adopté par un membre de la famille princière au pouvoir, il bénéficie entre autres des leçons de mathématiques et d'astronomie dispensées par Abu Nasr Mansur ibn-Ali ibn-Iraq (qui ne le connait pas ?). A l'âge de 17 ans, alors que la plupart de ses copains traînent dans les bars ou en boite de nuit, il s'amuse à déterminer la latitude de Kath à l'aide d'instruments de son invention, en mesurant la hauteur du Soleil. En 995, une guerre locale le pousse à partir en exil : il décide alors de s'installer en Iran, où il passera plusieurs années, dans la ville de Rayy (près de l'actuelle Téhéran).

Il y poursuit ses observations astronomiques et se lance dans l'écriture de plusieurs ouvrages, traitant aussi bien d'histoire que de mathématiques, comme "Les clés de l'astronomie", où il est avant tout question de trigonométrie. Il y entretient également une correspondance suivie avec nombre de philosophes et de savants, parmi lesquels figure un tout jeune homme qui deviendra l'un des plus grand médecins de son temps, Ibn Sīnā, plus connu en occident sous le nom d'Avicenne.
Aux alentours de l'an mille, Al-Biruni regagne sa patrie. Il se voit alors plus ou moins contraint de participer aux affaires publiques, et devient l'homme de confiance du calife Mamoun, qui lui confie à plusieurs reprises des missions diplomatiques, domaine où il semble faire preuve d'un certain talent. Hélas, tout cela ne dure qu'un temps et les nuages ne tardent pas à s'ammonceler dans le ciel du Khwarezm...

En 1016, Mamoun est assassiné au cours d'une révolte, ce qui permet au sultan Mahmud de Ghazna d'envahir la région, à la tête d'importantes forces militaires. Al-Biruni est emmené en captivité, dans les environs de l'actuelle Kaboul (Afghanistan). Ses compétences étant fort appréciées, il devient astrologue de la cour et se voit obligé d'accompagner le sultan dans ses expéditions militaires, ce qui le conduit jusqu'en Inde. Il va alors apprendre le sanskrit, et collecter une abondante documentation relative à ce pays dont on ignore presque tout. Il étudie ses habitants, leurs coutumes, leurs religions, qu'il relate dans un ouvrage qui fera date, "Le livre de l’Inde", achevé en 1030.
Mais venons-en aux faits : lors de son séjour en Inde, notre savant va mettre au point une méthode audacieuse permettant de déterminer la circonférence terrestre avec pour seul instrument un astrolabe
L'astrolabe est un instrument d'observation astronomique qui permet de mesurer la hauteur du Soleil et des étoiles, afin de déterminer l'heure. Son invention remonte à l'antiquité.. Pas besoin de voyager, pas besoin de chameaux, pas besoin d'assistants. Une seule contrainte cependant : il faut avoir à sa disposition une montagne qui ne soit ni trop petite, ni trop grande. Après en avoir déterminé la hauteur, il ne reste plus qu'à l'escalader et à mesurer, depuis son sommet, l'angle formé entre la direction horizontale et le point le plus éloigné visible à la surface de la Terre. A l'époque d'Al-Biruni, les tables trigonométriques permettant de calculer sinus, cosinus et tangentes sont au point, ce qui permet d'effectuer les calculs indispensables à l'exploitation des mesures. Regardons tout cela d'un peu plus près...

Première étape : calculer la hauteur de la montagne.

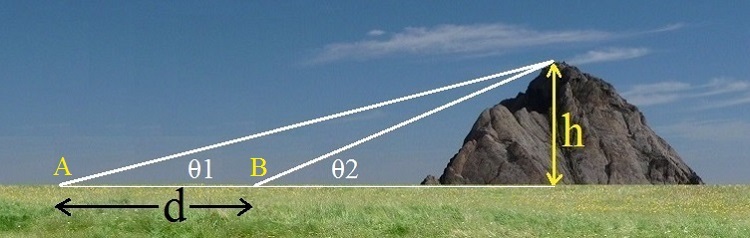
A l'aide d'un astrolabe, Al Biruni détermine la valeur des angles θ1 et θ2 entre la direction horizontale et le sommet de la montagne, et ce depuis deux points A et B séparés d'une distance d, qu'il mesure au préalable avec grande précision. La hauteur de la montagne s'obtient en appliquant la jolie formule que voici :

h = d.tanθ1.tanθ2 / (tanθ2 - tanθ1)    (1)

Si vous voulez savoir comment elle a été obtenue, rendez-vous ici !.

Deuxième étape : mesurer, depuis le sommet (S) de la montagne, l'angle α entre la direction horizontale et le point le plus éloigné de l'horizon (A).

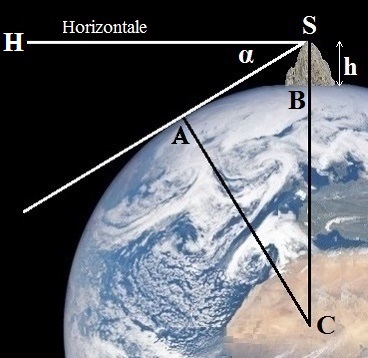
Le lien mathématique entre le rayon de la Terre (R_T) et la hauteur (h) de la montagne est le suivant (voir les détails du calcul ici !) :

R_T = h.cosα / (1 - cosα)

Il suffit donc, pour déterminer le rayon de la terre, de connaître la hauteur de la montagne depuis laquelle on mesure l'angle α, et le tour est joué.
En appliquant cette méthode, on estime qu'Al-Biruni aurait trouvé une valeur proche de 6340 km, soit un périmètre d'environ 39 810 km, ce qui n'est pas très éloigné des valeurs actuelles.

Bon, soyons honnêtes, il faut prendre ce résultat avec des pincettes. D'une part, nous ne savons pas exactement quelles unités de mesure il employa, d'autre part, la précision desdites mesures était entachée d'une foule d'incertitudes, dues entre autres à la réfraction atmosphérique, qui a pour effet de dévier les rayons lumineux, et plus particulièrement ceux qui rasent l'horizon, en raison de la plus grande épaisseur de l'atmosphère dans cette direction (c'est ce même phénomène qui est à l'origine des mirages). Si l'Histoire a retenu son nom, c'est donc avant tout pour l'élégance et la simplicité de la méthode employée, sans parler des nombreux ouvrages (près de 150 !) qu'il publia tout au long de sa vie. L'hommage que lui rendit en 1970 l'UAI (Union astronomique internationale), en attribuant le nom d'Al-Biruni à un cratère lunaire, est donc amplement justifié.

Mais il est temps de dire adieu à cet illustre savant et de poursuivre notre route. Nous allons dans le chapitre suivant effectuer un rapide survol d'une période de notre histoire trop souvent considérée comme synomyme de ténèbres et d'obscurantisme, et nous en profiterons pour tordre le cou à un préjugé qui a la vie dure...

Retour à l'introduction

Astronomie pour les myopes - Mentions légales