Faisons travailler nos neurones en douceur

Arghh... des calculs... mon Dieu, quelle horreur ! Rassurez-vous, ils sont extrêmement simples et largement à la portée de tout élève de lycée ayant quelques notions de mathématiques. Cela implique toutefois de ne pas avoir sèché trop souvent les cours, mais ça c'est une autre histoire...

Déterminer la hauteur d'une montagne par trigonométrie

Par définition :    tan θ1 = h / AC      soit :    AC = h / tan θ1

De même :    BC = h / tan θ2

On peut donc écrire :    d = AC - BC = h / tan θ1 - h / tan θ2 = h (1 / tan θ1 - 1 / tan θ2)

Soit :    d = h (tan θ2 - tan θ1) / (tan θ1 . tan θ2)=

Autrement dit :    h = d . tan θ1 . tan θ2 / (tan θ2 - tan θ1)

Déterminer le rayon de la Terre depuis le sommet d'une montagne

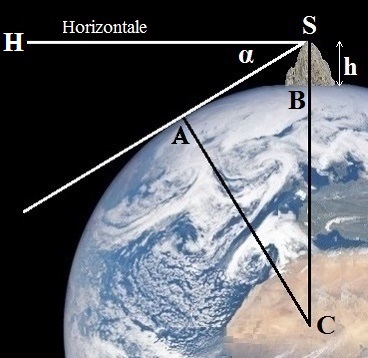
Démontrons que l'angle ˆSCA est égal à l'angle α :

ˆSCA + ˆCAS + ˆASC = 180°

L'angle ˆCAS est droit, donc :

ˆSCA + 90° + ˆASC = 180°, soit : ˆSCA + ˆASC = 90° (1)

L'angle ˆHSC est droit donc : ˆASC + α = ˆHSC = 90°

Soit : ˆASC = 90° - α (2)

De (1) et (2) on tire : ˆSCA + 90° - α = 90°

D'où : ˆSCA = α

Notons R_T le rayon de la Terre. On peut écrire :

cosα = cosˆSCA = CA / CS = CA / (CB + BS) = R_T / (R_T + h)

Soit : R_T = (R_T + h) . cos α

R_T - R_T . cosα = h . cos α

R_T (1 - cos α) = h . cos α

D'où : R_T = h . cos α / (1 - cos α)

Une fois que l'on a déterminé la hauteur de la montagne et la valeur de l'angle α, il ne reste plus qu'à appliquer la relation ci-dessus pour connaître le rayon de la Terre.

Astronomie pour les myopes - Mentions légales