Les lois de Kepler
En astronomie, les lois de Kepler sont les lois qui décrivent le mouvement des planètes autour du Soleil, des satellites autour de leurs planètes, et de façon générale le mouvement de tout corps céleste qui orbite autour d'un autre. Elles furent établies au début du XVIIe siècle par l'allemand Johannes Kepler, à partir des observations effectuées par l'astronome danois Tycho Brahé. Elles sont au nombre de trois, auxquelles on donne généralement le nom de loi des orbites, de loi des aires et de loi des périodes.
Première loi : la loi des orbites
"Les planètes décrivent des ellipses dont le Soleil occupe l'un des foyers".
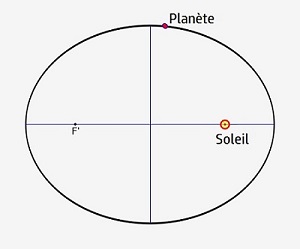
En réalité, ce n'est pas le Soleil mais le centre de masse qui occupe l'un des foyers. Toutefois, le Soleil étant beaucoup plus massif que les planètes, cela ne fait pas grande différence et l'on peut se contenter de cette approximation.
Deuxième loi : la loi des aires
"Le segment de droite qui relie le centre du Soleil au centre de la planète balaie des aires égales en des temps égaux".
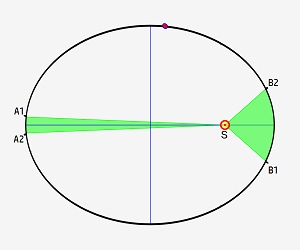
Précisons cela à l'aide d'un exemple. Sur l'image ci-dessus, la planète met la même durée pour passer de A1 à A2 que pour passer de B1 à B2 ; par conséquent, les 2 aires balayées ci-dessus sont égales.
Troisième loi : la loi des périodes
Cette loi est un peu plus compliquée. Elle dit que "le carré de la période de révolution d'une planète est proportionnelle au cube de la longueur du demi-grand axe de son orbite", le grand axe d'une ellipse étant son plus grand diamètre. Toutefois, les trajectoires des planètes étant très peu allongées, on peut considérer qu'elles sont pratiquement circulaires ; leur distance moyenne au Soleil peut donc être confondue avec leur demi-grand axe.
Exprimée mathématiquement, cela donne : T2 / a3 = k, ou k est une constante qui dépend des unités choisies. "T" correspond à la période de révolution de la planète et "a" au demi-grand axe de son orbite. Pour simplifier au maximum, exprimons "T" en années terrestres et "a" en unités astronomiques (ua). La constante k ayant la même valeur pour chaque planète (sinon, ça ne serait pas une constante), calculons sa valeur à l'aide de la planète Terre :
T2 / a3 = (1 an)2 / (1 ua)3 = 1 / 1 = 1 ; avec ce choix d'unités, la constante k vaut donc 1.
Exemple 1 : la planète Jupiter effectue sa révolution en 12 ans (à peu de chose
près). A quelle distance se trouve-t-elle donc du Soleil ?
Réponse : 122 / a3 = 1 , soit a3 = 122 = 144
Il ne reste qu'à extraire la racine cubique de 144, ce qui donne a = 5,2 unités astronomiques
Exemple 2 : la planète Saturne se trouve à 9,5 unités astronomiques du Soleil.
Quelle est sa période de révolution ?
Réponse : T2 / 9,53 = 1 , soit T2 = 9,53 = 857
Extrayons la racine carrée de 857. Cela donne : T = 29,3 ans
Astronomie pour les myopes -
Mentions légales